728x90

1003번 / 피보나치 함수

❓ 피보나치 함수

🏷️ 관련 주제 : Dynamic Programming

💦 나의 시도

int fibonacci(int n) {
    if (n == 0) {
        printf("0");
        return 0;
    } else if (n == 1) {
        printf("1");
        return 1;
    } else {
        return fibonacci(n‐1) + fibonacci(n‐2);
    }
}

n이 0 일 때, int `zero` 1 증가, n이 1일 때, int `one` 1증가하는 `fibonacci()` 메서드 만들기

인스턴스 변수 선언
- public static int zero : 0이 출력되는 횟수를 할당할 변수
- public static int one : 1이 출력되는 횟수를 할당할 변수
void fibonacci(int n) 메서드 정의
- n이 0이면 zero 1 증가
- n이 1이면 one 1 증가
- 그 외의 경우, fibonacci(n - 1), fibonacci(n - 2) 실행
테스트 케이스 개수 int T를 입력받아 할당
0 ~ (T - 1) 범위에서 반복문을 돌면서 fibonacci(n)의 n 입력 받기
zero 0으로 초기화
one 0으로 초기화
fibonacci(n) 실행
BufferedWriter에 (0이 출력된 횟수) + " " + (1이 출력된 횟수) + "\n" 쓰기
반복문이 끝난 후에 BufferedWriter의 close() 메서드 실행하며 결과값 출력

위의 방법으로 작성한 코드

import java.io.*;

public class Main {
    public static int zero;
    public static int one;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        int T = Integer.parseInt(br.readLine());

        for (int i = 0; i < T; i++) {
            int n = Integer.parseInt(br.readLine());
            zero = 0;
            one = 0;
            fibonacci(n);
            bw.write(zero + " " + one + "\n");
        }

        bw.close();
    }

    public static void fibonacci(int n) {
        if (n == 0) {
            zero++;
        } else if (n == 1) {
            one++;
        } else {
            fibonacci(n - 1);
            fibonacci(n - 2);
        }
    }
}

⏱️ 시간 초과

피보나치 수열을 테스트 케이스마다 일일이 새로 구하는 것 때문인 것 같아서 풀이 방법 수정

테스트 케이스를 입력 받고 가장 큰 값에 대해서 피보나치 수를 구한 후, 각 결과값 출력

테스트 케이스를 담을 Queue numbers 초기화
테스트 케이스 개수 int T를 입력 받아 할당
테스트 케이스 중 가장 큰 값 int maxN을 0으로 초기화
0 ~ (T - 1) 범위를 반복문을 돌면서 테스트 케이스 int n을 입력 받아 numbers에 추가하고 maxN에 maxN과 n 중 큰 값 할당
N에 대하여 0과 1의 출력 횟수를 담을 길이 (maxN + 1)인 이차원 배열 int[][] fibonacci01를 선언
fibonacci01[0][0], fibonacci01[1][1]에 1을 할당

반복문의 인덱스 int i가 2인 경우부터 maxN인 경우까지 fibonacci(N)의 0과 1의 출력 횟수 구하기

  fibonacci01[i][0] = fibonacci01[i - 1][0] + fibonacci01[i - 2][0];
  fibonacci01[i][1] = fibonacci01[i - 1][1] + fibonacci01[i - 2][1];

numbers의 원소를 for-each문으로 꺼내 int n에 할당
int[] zeroOne에 fibonacci01[n]을 할당 : n번째 피보나치 수에서 출력되는 {0의 횟수, 1의 횟수}
BufferedWriter에 0과 1의 출력 횟수를 공백으로 구분하여 쓰고 마지막에 줄바꿈 추가
- bw.write(zeroOne[0] + " " + zeroOne[1]+"\n");
BufferedWriter의 close() 메서드 실행하며 결과값 출력하기

💥 런타임 에러 (ArrayIndexOutOfBounds)

테스트 케이스를 직접 만들어 오류 부분 찾기

1
0

여기서 Exception in thread "main" java.lang.ArrayIndexOutOfBoundsException: Index 1 out of bounds for length 1 at Main.main(Main.java:20) 발생

int[][] fibonacci01 = new int[maxN + 1][2];
fibonacci01[0][0] = fibonacci01[1][1] = 1;

여기서 maxN이 1 미만인 경우, fibonacci01의 길이가 1이 되어 최대 인덱스가 0인데
그 아래에서 fibonacci01[1][1]에 1을 할당하고 있어서
ArrayIndexOutOfBoundsException 발생

코드를 다음과 같이 수정

int[][] fibonacci01 = new int[Math.max(maxN + 1, 2)][2];

📑제출 기록 및 오답 원인

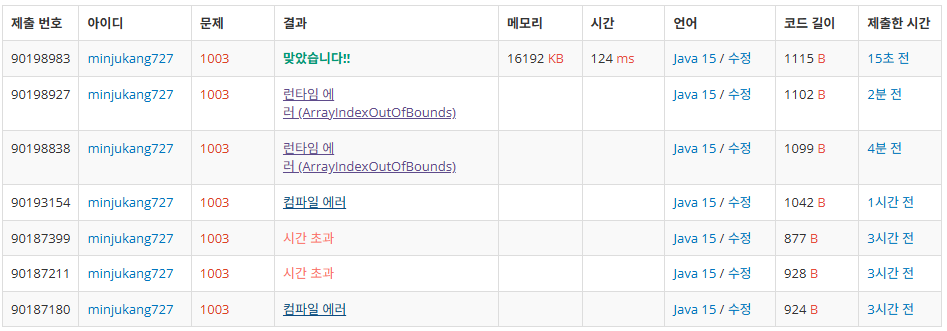
💯 해결 방법

import java.io.*;
import java.util.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        Queue<Integer> numbers = new LinkedList<>();
        int T = Integer.parseInt(br.readLine());
        int maxN = 0;

        for (int i = 0; i < T; i++) {
            int n = Integer.parseInt(br.readLine());
            numbers.add(n);
            maxN = Math.max(maxN, n);
        }

        int[][] fibonacci01 = new int[Math.max(maxN + 1, 2)][2];
        fibonacci01[0][0] = fibonacci01[1][1] = 1;

        for (int i = 2; i < maxN + 1; i++) {
            fibonacci01[i][0] = fibonacci01[i - 1][0] + fibonacci01[i - 2][0];
            fibonacci01[i][1] = fibonacci01[i - 1][1] + fibonacci01[i - 2][1];
        }

        for (int n : numbers) {
            int[] zeroOne = fibonacci01[n];
            bw.write(zeroOne[0] + " " + zeroOne[1]+"\n");
        }

        bw.close();
    }
}

✍️ 오늘 공부한 내용

동적 계획법(DP; Dynamic Programming)

작은 문제들을 풀면서 그 결과를 저장해 나아가면서 전체 문제를 해결하는 알고리즘을 의미합니다.

중복 계산을 줄여서 계산 속도를 높일 수 있으며
경우의 수가 많은 경우에도 효율적으로 계산할 수 있습니다.
일반적으로 재귀적으로 구현되며
메모이제이션(Memoization) 기법을 사용하여 중복 계산을 피합니다.

재귀(Recursion)

자기 자신을 호출하는 함수로 반복적으로 호출을 함으로써 원하는 결과를 도출할 수 있습니다.

메모이제이션(Memoization)

'중복 계산'을 피하기 위한 기법
이전에 계산된 결과를 저장하고 다음에 동일한 계산이 필요할 때, 저장된 결과를 이용하여 중복 계산을 피함으로써 성능을 향상시킬 수 있습니다.

메모이제이션 구성 과정

입력값에 대한 결과값을 저장할 메모이제이션 테이블을 초기화합니다.
함수를 호출할 때, 먼저 메모이제이션 테이블에서 해당 입력값의 결과값이 이미 저장되어 있는지 확인합니다.
저장되어 있으면 해당 결과값을 반환하고,
저장되어 있지 않으면 계산을 수행하고 그 결과를 메모이제이션 테이블에 저장합니다.
계산된 결과값을 반환합니다.

메모이제이션 테이블

동적 계획법에서 사용되는 저장 공간
일반적으로 해시 테이블이나 배열 등을 사용하여 구현합니다.

동적 계획법의 조건

최적 부분 구조(Optimal Substructure)
- 큰 문제의 최적해가 작은 문제의 최적해를 포함하는 성질
- 즉, 작은 문제의 최적해를 구한 후 그것을 이용하여 큰 문제의 최적해를 구할 수 있습니다.
중복 부분 문제(Overlapping Subproblems)
- 동일한 작은 문제를 반복적으로 해결해야 하는 성질
- 즉, 작은 문제를 해결할 때 반복적으로 같은 문제를 해결해야 합니다.

동적 계획법 구현

문제를 하위 문제로 쪼갭니다.
하위 문제를 재귀적으로 해결합니다.
결과를 저장합니다.(Memoization)
저장된 결과를 이용하여 큰 문제를 해결합니다.

동적 계획법의 종류

탑다운(Top-Down)

재귀적으로 호출하여 문제를 해결
큰 문제를 작은 문제로 나누어 푸는 분할 정복(Divide and Conquer) 방식과 비슷
단, 중복되는 작은 문제들을 한 번만 푸는 것이 특징
장점 : 작은 문제들의 결과값을 저장함으로써 동일한 계산을 반복하지 않아 시간 복잡도 감소
단점 : 재귀 함수 호출을 사용하므로 스택 오버플로(Stack Overflow) 문제가 발생할 수 있습니다.

스택 오버플로(Stack Overflow)

함수 호출 시, 스택 메모리에 할당된 공간을 벗어나게 되는 현상
일반적으로 재귀 호출이 지나치게 많이 일어날 때 발생
프로그램이 비정상적으로 종료

재귀적으로 수행하는 피보나치 수열 vs 탑다운 방식
- 피보나치 수열 : 앞의 두 수를 더해가는 방법으로 재귀적으로 수행하지만 중복 계산이 발생하여 비효율적
- 탑다운 방식 : 중복되는 작은 문제들을 한번만 풀기에 상대적으로 효율적

바텀업(Bottom-Up)

작은 문제부터 해결하여 큰 문제까지 해결하는 알고리즘 방식
이전에 계산한 부분 문제의 결과를 저장해두고 나중에 같은 부분 문제가 나타날 때 다시 계산하지 않고 저장된 값을 사용하여 시간을 절약
탑다운 방식과 비교하여 재귀적으로 수행하지 않고 '반복문'을 통하여 문제를 해결해 나아가는 방식

탑다운 방식 vs 바텀업 방식

둘 다 동일한 계획적 탐색의 종류 중에 하나지만 각각 해결방식이 다름

- 탑다운 방식 : 작은 부문 문제를 '재귀적인 호출'을 이용하여서 해결하는 방식
- 바텀업 방식 : 작은 부분 문제부터 시작하여 '반복문'을 통해 해를 계산하고 저장해둔 뒤 이전에 계산 문제의 해를 점점 더 큰 문제로 해결하는 방식

동적 계획법 적용 가능한 문제

피보나치 수열(Fibonacci numbers)
- 이전 두 항의 합이 다음 항의 합이 되는 수열
최장 공통 수열(Longest Common Subsequence, LCS)
- 두 개의 문자열이 주어졌을 때, 두 문자열에서 '공통'으로 나타나는 '가장 긴 부분 문자열'을 찾는 문제
- ex) 'ABCDGH'와 'AEDFHR'의 LCS는 'ADH'
- 바텀업 방식을 이용하여 해결
최장 공통 문자열(Longest Common Substring)
- 두 개의 문자열 내에서 '연속적인 부분 문자열' 중 가장 긴 길이의 공통 부분 문자열을 찾는 문제
- 연속되는 문자열인 경우를 찾음
- ex) 'banaan'와 'vbankn'의 최장 공통 문자열은 'ban'
최장 증가 부분 수열(Longest Increasing Subsequence, LIS)
- 주어진 수열에서 일부 항목을 선택하여 만들 수 있는 부분 수열 중, '원소의 크기가 증가하는 순서대로 정렬'되어 있는 가장 긴 수열을 찾는 문제
- ex) [10, 22, 9, 33, 21, 50, 41, 60, 80]의 LIS는 [10, 22, 33, 50, 60, 80]
최장 감소 부분 수열(Longest Decreasing Subsequence, LDS)
- 주어진 수열에서 일부 항목을 선택하여 만들 수 있는 부분 수열 중에서, '원소의 크기가 감소하는 순서대로 정렬'되어 있는 가장 긴 수열을 찾는 문제
- ex) [80, 60, 50, 41, 33, 22, 21, 10, 9]의 LDS는 [80, 60, 50, 41, 33, 22, 21, 10, 9]

🏷️ 문제 풀면서 참고한 블로그

[Java/알고리즘] 동적 계획법(DP: Dynamic Programming) 이해하기

728x90

저작자표시 비영리 변경금지 (새창열림)

[백준 | Java] 1003번 피보나치 함수 - Dynamic Programming

❓ 피보나치 함수

💦 나의 시도

n이 0 일 때, int `zero` 1 증가, n이 1일 때, int `one` 1증가하는 `fibonacci()` 메서드 만들기

⏱️ 시간 초과

테스트 케이스를 입력 받고 가장 큰 값에 대해서 피보나치 수를 구한 후, 각 결과값 출력

💥 런타임 에러 (ArrayIndexOutOfBounds)

📑제출 기록 및 오답 원인

💯 해결 방법

✍️ 오늘 공부한 내용

동적 계획법(DP; Dynamic Programming)

재귀(Recursion)

메모이제이션(Memoization)

메모이제이션 구성 과정

메모이제이션 테이블

동적 계획법의 조건

동적 계획법 구현

동적 계획법의 종류

탑다운(Top-Down)

스택 오버플로(Stack Overflow)

바텀업(Bottom-Up)

탑다운 방식 vs 바텀업 방식

동적 계획법 적용 가능한 문제

🏷️ 문제 풀면서 참고한 블로그

티스토리툴바

[백준 | Java] 1003번 피보나치 함수 - Dynamic Programming

❓ 피보나치 함수

💦 나의 시도

n이 0 일 때, int zero 1 증가, n이 1일 때, int one 1증가하는 fibonacci() 메서드 만들기

⏱️ 시간 초과

테스트 케이스를 입력 받고 가장 큰 값에 대해서 피보나치 수를 구한 후, 각 결과값 출력

💥 런타임 에러 (ArrayIndexOutOfBounds)

📑제출 기록 및 오답 원인

💯 해결 방법

✍️ 오늘 공부한 내용

동적 계획법(DP; Dynamic Programming)

재귀(Recursion)

메모이제이션(Memoization)

메모이제이션 구성 과정

메모이제이션 테이블

동적 계획법의 조건

동적 계획법 구현

동적 계획법의 종류

탑다운(Top-Down)

스택 오버플로(Stack Overflow)

바텀업(Bottom-Up)

탑다운 방식 vs 바텀업 방식

동적 계획법 적용 가능한 문제

🏷️ 문제 풀면서 참고한 블로그

관련글

티스토리툴바

n이 0 일 때, int `zero` 1 증가, n이 1일 때, int `one` 1증가하는 `fibonacci()` 메서드 만들기