❓ 주사위 윷놀이
🏷️ 관련 주제 : DFS Brute Force
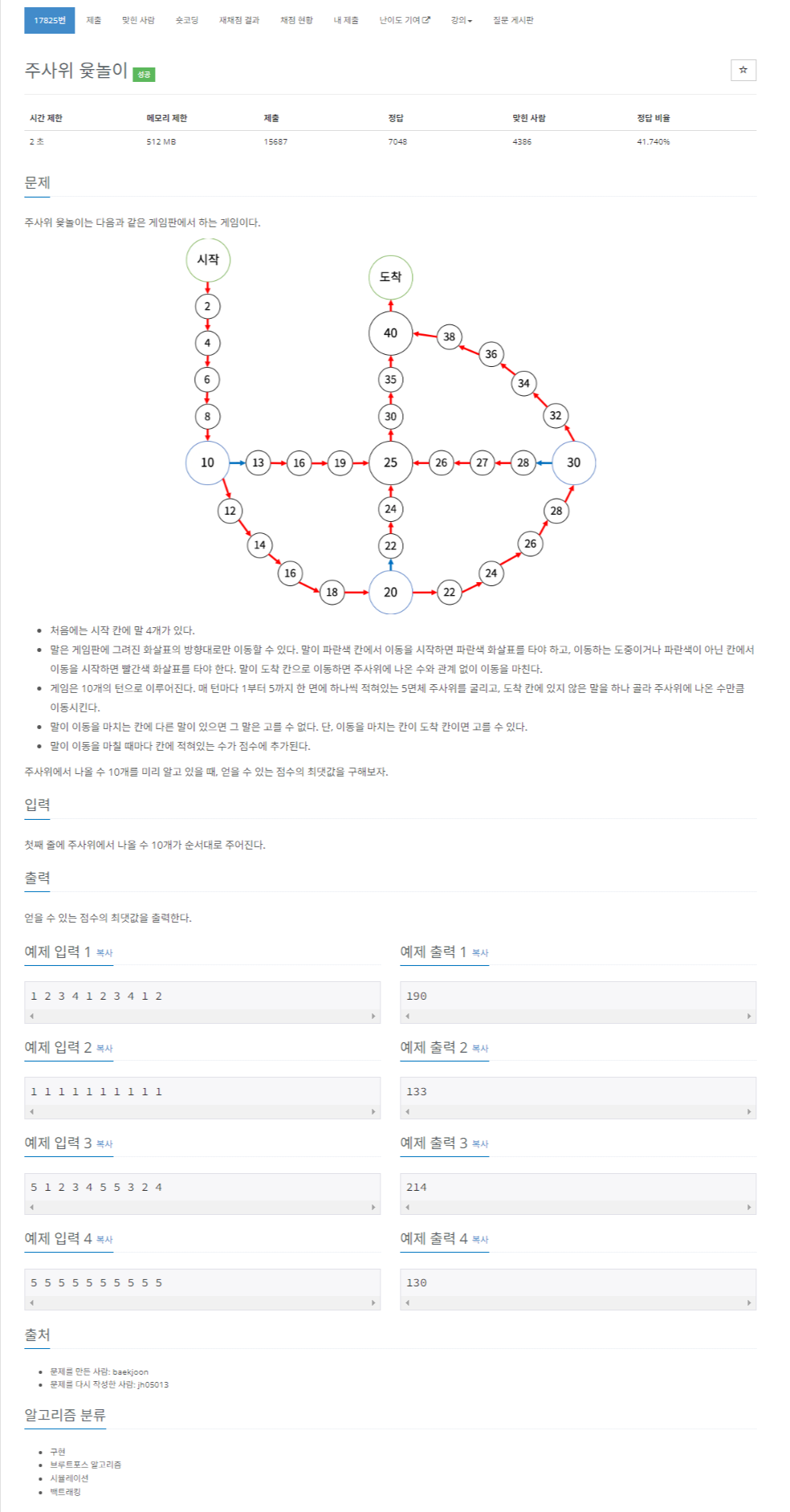
💦 나의 시도
윷놀이(Small) 문제를 해결한 것에 용기를 얻어 그와 비슷한 방식으로 이번 문제도 풀어보기로 하였습니다.
말 이동은 getEnd()메서드에서 switch-case문 및 재귀함수를 통해 말이 이동한 위치의 번호를 가져오도록 하였고
DFS를 통해 최대 점수를 구하였습니다.
각 말의 위치를 쉽게 알기 위해 Map<Integer, Integer> 자료구조를 활용하여 현재 말의 위치를 저장하였고
던져 나온 주사위의 크기를 Queue에 저장하여 FIFO 원칙으로 이동 칸 수를 하나씩 뽑아서 탐색을 진행하였습니다.
처음 입력값을 넣어 코드의 실행 결과를 출력해 본 결과 값이 너무 크게 나오는 문제가 발생하였습니다.
그래서 코드 중간 중간에 출력 값을 넣어 값이 어떻게 나오는지 살펴보며 코드를 수정하였는데
알고보니 score 변수에 DFS 탐색 결과를 그대로 할당하여 다음 탐색 시, 잘못된 score 값을 매개변수로 받아서 그런 것이었습니다.
따라서 int maxScore라는 변수를 하나 생성하여dfs() 메서드 호출 결과와 maxScore값을 비교하여 maxScore에 재할당하여 최댓값은 다른 변수에 구분하여 할당하고score 변수는 그대로 매개변수로 주어 같은 Level 탐색 시, 같은 score 값을 매개변수로 받을 수 있도록 하였습니다.
int maxScore = score;
if (!moves.isEmpty()) {
Set<Integer> keys = new HashSet<>(horses.keySet());
for (int key : keys) {
Map<Integer, Integer> copyHorses = new HashMap<>(horses);
Queue<Integer> copyMoves = new LinkedList<>(moves);
int score2 = dfs(copyHorses, copyMoves, key, score);
// 이전의 잘못된 코드 : score = Math.max(score, score2);
maxScore = Math.max(maxScore, score2);
}
}📑제출 기록 및 오답 원인

💯 해결 방법
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
Queue<Integer> moves = new LinkedList<>();
for (int i = 0; i < 10; i++) {
moves.add(Integer.parseInt(st.nextToken()));
}
Map<Integer, Integer> horses = new HashMap<>(Map.of(0, 4));
System.out.println(dfs(horses, moves, 0, 0));
}
public static int dfs(Map<Integer, Integer> horses, Queue<Integer> moves, int curIdx, int score) {
int move = moves.peek();
int nextIdx = getEnd(curIdx, move);
if (horses.containsKey(nextIdx)) {
return 0;
}
moves.poll();
if (curIdx == 0) {
int cnt = horses.get(curIdx);
if (cnt == 1) {
horses.remove(curIdx);
} else {
horses.put(curIdx, cnt - 1);
}
} else {
horses.remove(curIdx);
}
if (nextIdx != 42) {
horses.put(nextIdx, 1);
}
if (nextIdx >= 16 * 3) {
score += nextIdx / 3;
} else if (nextIdx != 42) {
score += nextIdx;
}
int maxScore = score;
if (!moves.isEmpty()) {
Set<Integer> keys = new HashSet<>(horses.keySet());
for (int key : keys) {
Map<Integer, Integer> copyHorses = new HashMap<>(horses);
Queue<Integer> copyMoves = new LinkedList<>(moves);
int score2 = dfs(copyHorses, copyMoves, key, score);
maxScore = Math.max(maxScore, score2);
}
}
return maxScore;
}
public static int getEnd(int start, int move) {
if (move == 0) {
return start;
}
switch (start) {
case 10 : return getEnd(13, move - 1);
case 13 : return getEnd(16 * 3, move - 1);
case 16 * 3 : return getEnd(19, move - 1);
case 19: return getEnd(25, move - 1);
case 20 : return getEnd(22 * 3, move - 1);
case 22 * 3 : return getEnd(24 * 3, move - 1);
case 24 * 3 : return getEnd(25, move - 1);
case 25 : return getEnd(30 * 3, move - 1);
case 30 * 3 : return getEnd(35, move - 1);
case 35 : return getEnd(40, move - 1);
case 30 : return getEnd(28 * 3, move - 1);
case 28 * 3 : return getEnd(27, move - 1);
case 27 : return getEnd(26 * 3, move - 1);
case 26 * 3 : return getEnd(25, move - 1);
case 40 : return 42;
default :
int end = start + move * 2;
if (end >= 42) {
return 42;
}
return end;
}
}
}📝 공부한 내용
백트래킹(Back Tracking)
재귀적으로 문제를 하나씩 풀어나가되
현재 재귀를 통해 확인 중인 상태(노드)가 제한 조건에 위배되는지 판단하고
그러한 경우 해당 상태(노드)를 제외하고 다음 단계로 나아가는 방식
- 현재 상태(노드)에서 다음 상태(노드)로 나아갈 수 있는 모든 경우를 찾되,
그 중 유망하지 않다면 현재에서 더 나아가지 않고
이전 상태로 돌아가 다음 상태(노드)를 검사한다. - 이를 통해 모든 경우의 수를 체크하지 않고 필요한 것만 체크하여 전체 풀이 시간을 단축할 수 있게 된다.
가지치기(pruning)
더 이상 탐색할 필요가 없는(유망하지 않은) 상태(노드)를 제외하는 것
시간 복잡도
Exponential(지수, $2^n$꼴)
백트래킹을 사용하는 대표적인 알고리즘
DFS: 재귀를 통해 가능한 경로 중 유망한 경로만 찾아서 탐색을 수행한 뒤, 다시 돌아와 그 중 가장 최적 경로를 반환
해결할 수 있는 문제
- 의사 결정
- 최적화
- 열거하기
사실 사용 가능한 경우가 많지만 대부분 Dynamic Programming, Greedy 알고리즘 등으로 더 빠르게 해결 가능하다.
하지만 일부 경우의 문제들은 백트래킹으로만 해결 가능한 문제도 있으며
그러한 경우 많이 사용된다.
그리디 알고리즘(Greedy)
부분 최적해를 구해 전체 최적해를 도출하는 알고리즘
백트래킹을 통해 추가 점검을 하지 않고 현재 조건에서 선택했다면 더 이상 다른 선택 가능 경우는 검증하지 않음.

그럼에도 불구하고 속도가 매우 빠르기 때문에 다음 두 조건을 만족하는 경우 자주 사용될 수 있다.
Greedy 적용 조건
1) 탐욕 선택 속성(Greedy Choice Property)
- 이전 선택이 이후에 영향을 주지 않음.
2) 최적 부분 구조(Optimal Substructure)
- 부분 문제의 최적 결과가 전체에도 그대로 적용될 수 있어야 한다.2의 조건에서 DP(Dynamic Programming)을 떠올릴 수 있지만
DP의 경우 1번 조건을 만족하지 않는다.
Greedy 문제임을 증명하는 방법
반례를 1개만 찾으면 OK!
Greedy를 이용해 해결할 수 있는 문제 예시
활동 선택(Action Selection) 문제
N개의 활동이 있고 각 활동에는 시작 시간 및 종료 시간이 있을 때,
한 사람이 최대한 많이 할 수 있는 활동(Activity)의 수를 구하는 문제
즉, 각각의 활동(Activity)에는 시간이 소요되므로 하나를 선택했다면 그 동안 해당 시간에 다른 활동을 할 수 없다.
이러한 상황일 때 가장 많은 활동에 참여하려면 어떻게 해야할까?
Solution
언제 시작하든 전체에서 가장 종료 시간이 빠른 것부터 선택해야 한다.
(어차피 시작 시간은 종료 시간 이전이므로 고려하지 않는다.)
따라서 종료 시간을 기준으로 정렬한 뒤,
제일 먼저 끝나는 활동을 무조건 선택하고 끝났을 때,
바로 다음에 선택할 수 있는 활동을 찾아 수행하는 방식을 반복하여 해결할 수 있다.
🏷️ 문제 풀면서 참고한 블로그




